Hardware
Cpu page
Motherboard page
Video Card page
Sneak
Peak page
Programming
Disclaimer:
It's really a shame that i have
to even write this , but here it goes: I am not responsible for any damage
that this page has caused you , your dog , you wife your
boss , your time , your web browser , your computer , your life , your
mom , etc... you view everything on this page at your own risk. I
am not responsible for any spelling
errors , wrong facts , lies (not that you'll find any). All opinions
are of the person who
wrote them , and remember , they are only opinions so you dont have to
kill someone because
they disagree with you. Lastly , all the graphics and content on this page
are
Background: Evaluating an expression has been a problem
for many years , and many solutions have been devised. The solution we
will run through will require converting the Infix expression (Infix meaning
the operator is in between the 2 operands ) into PostFix (the operator
is after the 2 operands) and evaluate it. This version will only deal with
binary operators (those that take 2 operands) , however , adding unary
operators is a trivial task.
Step 1 , Converting INFIX to POSTFIX
I will assume that the reader knowledgeable in programming , since i will not discuss syntax and much code. Also , the reader should be familiar with the STACK datatype. I will discuss it breifly in this section , however a more detailed explanation will appear in the General Programming Info Section under DATATYPES , coming soon!
CONTENTS:
What is a Stack?
The basic Idea
Why it works
Dealing with Parenthesis
Evaluating PostFix expressions
A Stack is a simple data type in which items are inserted
on the top , and removed from the top. This is the only way data can enter
or exit the stack. (From the top) An example of a stack would be a stack
of books. Take 1 book , put it on a table , then take another book and
put it on top of the last book , this is called PUSHING the book onto the
stack. PUSH is one of the basic Stack functions. It takes the element passed
to it and adds it to the TOP of the stack (Always the top) Now , take off
the book you just added. This is called POPING , pop removes the element
on the Top of the stack. As you may already see , if Someone were to PUSH(add)
5 elements on to a stack (lets say A,B,C,D,E) And then POPed them all off
, he would get them back in reverse order. Thus a Stack is usefull when
we want to reverse "stuff". Also , keep that in mind. Well , that's enough
for stacks , on to the good stuff (How to use the stacks!)
Back to Contents
In order to solve this rather complicated problem , we will start with a simple implementation with NO parenthesis (adding parenthesis is trivial). The solution to this problem is not at all as hard as coming up with the solution. Here is the basic algorithm in words for converting INFIX to POSTFIX without parenthesis. You will notice that stacks come into play here.
While there are still characters in the string
Read a character
If it is an
operand , push it in the answer STACK
If it is an
operator ,
while not Precedence of currentOperator is <= POP(OperatorStack)
push the POPed operator into answer stack
end loop
Push currentOperator into OperatorStack
end loop
Flush OperatorStack into Answer
thats it!! , Believe it or not , thats the basic idea , and it works!
In order for you to see why this works , we must observe
a few basic things about POSTFIX notation.
One important fact is that Postfix doesnt ever contain
or need parenthesis. Which will come in play in the Adding parenthesis
section and Evaluating PostFix section. Secondly , The OPERANDS in the
POSTFIX expression are in the SAME ORDER as those in the INFIX expression.
This is why , in the above code , if we get an operand , we automatically
push it into the STACK because it is in order. The STACK is used because
it provides an easy way to store and retreive the information in an organized
manner. Since the Operands go in the same place as the INFIX , all we have
to do is find out where to put the OPERATORS. Lets examine the following
example: 1+2. Simple huh? Let's find out...
In order to do this with our algorithm , we will first take the '1'. Since its an Operand , we put it in the answer stack. so far everything looks like this
1
ANSWER STACK OPERATORSTACK
Now , we take the next character , a '+'. Since this is an Operator , we don't know what to do with it yet , so lets dump it into the OperatorStack , so now everything looks like this.
1
+
ANSWERSTACK OPERATORSTACK
Now , we hit a '2' , so we do the same as we did with the one.
2
1
+
ANSWERSTACK OPERATORSTACK
Now , since we are all pro's at converting infix2Postfix
, we know that the answer is 12+
so we will just push the + in operatorstack onto answerstack
, yeilding
+
2
1
ANSWERSTACK , and because this is in reverse order (a
Stack , when taken out , it gives us
12+ , which is what we want! Is that it? I don't think
so... Let's try this example , 1*2+3. Using what we would get what the
graphic below illustrates.
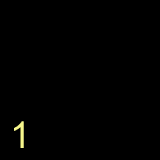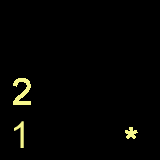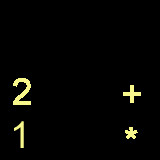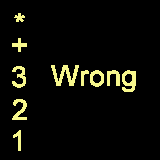
Dealing with parenthesis may be difficult , however , once we will analyze the situation and what parenthesis actually do , we will see it is a very trivial task. (Approx 2 or 3 lines of code). What the parenthesis actually do: After you look carefully at what parenthesis do , you will notice that parenthesis act like the highest precedence value. If you remember how we treated the highest order operator in our stack above , you will see how easy it is to deal with parenthesis. Since the parenthesis always have a higher precedence than the object before , the parenthesis will always go on top of the stack. (Simple huh?) So , all we have to do is make sure the parenthesis block goes on top. And how do we do this? There are many ways... One way is to this like so. If you encounter a '(' , you raise the precedence of the next operators by some number which will raise it by a 'degree' (if you have operators with precedence ranging from 1-3 , then you would have to add at least 4...) Then , you proceed as normal , until you hit a closing partenthesis (')') , in this case you subtract the 4 you added. Simple.
Evaluating POSTFIX expressions
Evaluating Postfix expressions is a very simple task. As a matter of fact , you may have even figured it out your self! (Stacks...Stacks...Stacks...)
Here is the Algorithm to evaluate postfix expressions. It is very simple and i don't think you will need any further explanation. If you don't get it at first , try it in your head , and if you STILL don't get it , E-mail me
{ This CODE ASSUMES THAT THE POSTFIX EXPRESSION IS VALID! }
While (Characters in POSTFIX expression)
{
Get Char
If ( Operand ) // number...
Push into
AnswerStack;
If (Operator) //+,-,*,/
Pop 2 elements
from AnswerStack
Operate(Operator_you_just_got
, PoppedItem1,PoppedItem2);
} //end while loop;